浮点数转化成二进制

1、浮点数在计算机中是如何表示的

学过《计算机组成原理》或者类似《计算机系统》这些课程的小伙伴们应该都知道，浮点数在计算机中的存储方式遵循IEEE 754浮点数计数标准，可以表示为：

1.M... * 2 ** E

上述的就是 尾数 + 阶码 的编码方式，说的通俗一点就是类似于数学课本上的科学计数法表示方式：有效数字 + 指数位。

因此，只要给出：符号（S）、阶码部分（E）、尾数部分（M） 这三个维度的信息，一个浮点数的表示就完全确定下来了，所以float和double这两种类型的浮点数在计算机中的存储结构就表示成下图所示这样子：

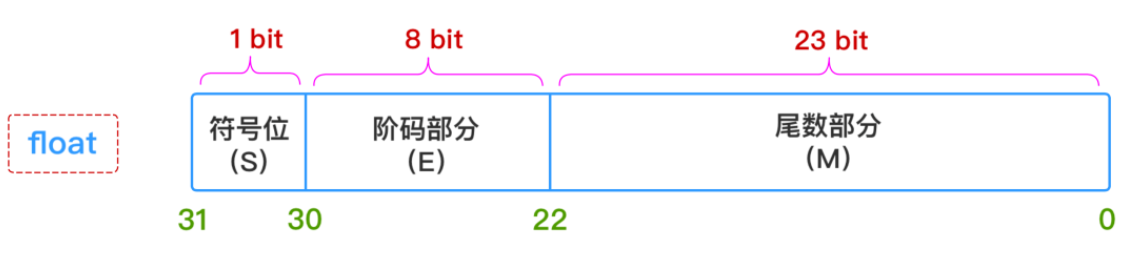
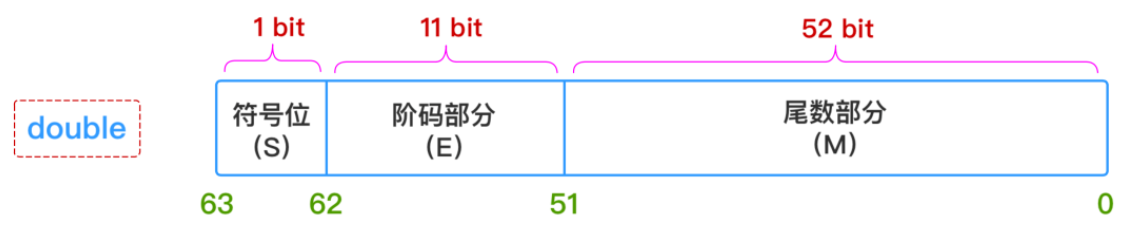
1. 符号部分（S）

   • 0:正
   • 1:负

2. 阶码部分（E）（指数部分）：

   • 对于float型浮点数，指数部分8位，考虑可正可负，因此可以表示的指数范围为 -127~128
   • 对于double型浮点数，指数部分11位，考虑可正可负，因此可以表示的指数范围为 -1023~1024

   负指数决定了浮点数所能表达的绝对值最小的非零数；而正指数决定了浮点数所能表达的绝对值最大的数，也即决定了浮点数的取值范围。所以：

   • float 的范围为 -2^128 ~ +2^128，也即 -3.40E+38 ~ +3.40E+38。
   • double的范围为 -2^1024 ~ +2^1024，也即 -1.79E+308 ~ +1.79E+308。

3. 尾数部分（M）。浮点数的精度是由尾数来决定的：

   • 对于float型浮点数，尾数部分23位，换算成十进制就是 2^23 = 8388608，一共7位，这意味着最多能有7位有效数字，但绝对能保证的为6位，也即十进制精度只有 6~7 位。
   • 对于double型浮点数，尾数部分52位，换算成十进制就是 2^52 = 4503599627370496，同理，十进制精度只有 15~16 位。
     所以，浮点数交给计算机存储的时候，可能会有精度丢失问题！！！因此，使用时要格外小心，如果因为这一块除了bug，定位问题还是非常艰难的，所以预防工作要做好。

2、二进制和十进制转化

float型 十进制转化为二进制格式

1. 先将这个实数的绝对值化为二进制格式，注意实数的整数部分和小数部分的二进制方法不同。
2. 将这个二进制格式实数的小数点左移或右移n位，直到小数点移动到第一个有效数字的右边。
3. 从小数点右边第一位开始数出二十三位数字放入第22到第0位。
4. 如果实数是正的，则在第31位放入“0”，否则放入“1”。
5. 如果 n 是左移得到的，说明指数是正的，第30位放入“1”。如果n是右移得到的或n=0，则第30位放入“0”。
6. 如果 n 是左移得到的，则将n减去1后化为二进制，并在左边加“0”补足七位，放入第29到第23位。如果n是右移得到的或n=0，则将n化为二进制后在左边加“0”补足七位，再各位求反，再放入第29到第23位。

float 型 二进制转化为十进制

1. 将第22位到第0位的二进制数写出来，在最左边补一位“1”，得到二十四位有效数字。将小数点点在最左边那个“1”的右边。
2. 取出第29到第23位所表示的值n。当30位是“0”时将n各位求反。当30位是“1”时将n增1。
3. 将小数点左移n位（当30位是“0”时）或右移n位（当30位是“1”时），得到一个二进制表示的实数。
4. 将这个二进制实数化为十进制，并根据第31位是“0”还是“1”加上正号或负号即可。

3、进制转换计算案例

把十进制小数0.875转换成二进制

可以分以下几步：

1. 以小数点为界，拆分；

2. 整数部分转换：整数转二进制使用 除2取余法 即可。0.875 整数部分为0，无需操作；

3. 小数部分转换：小数部分的转换不同于整数部分，采用的是 “乘2取整法”。
   

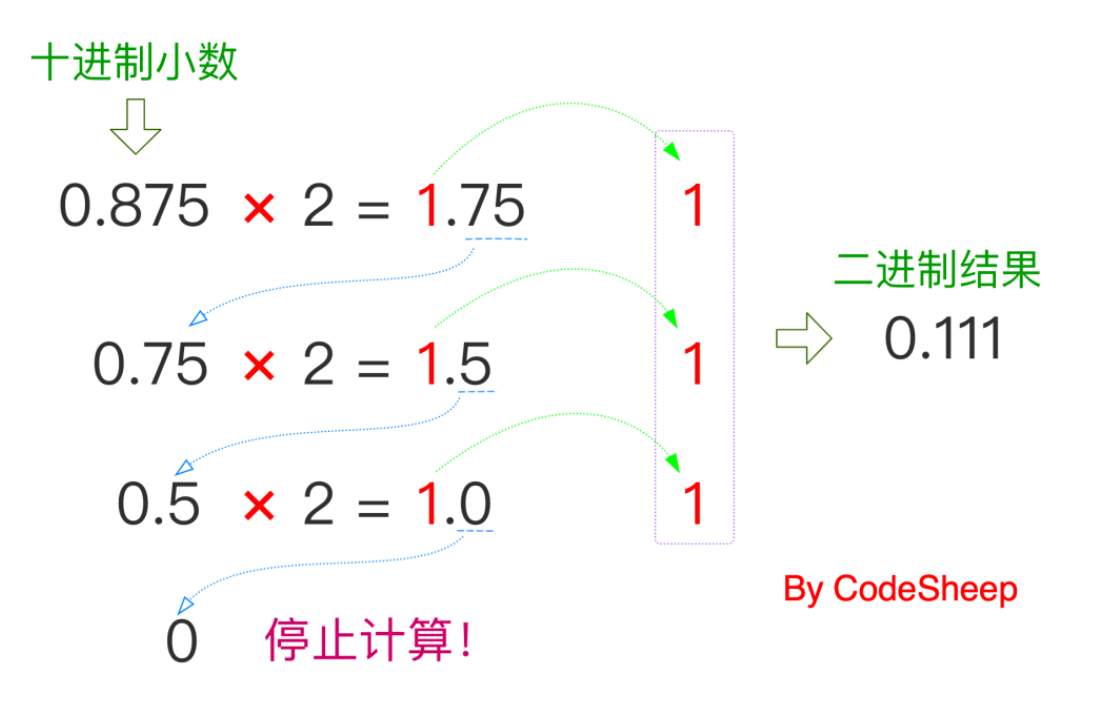
   注意：“乘2取整法”当结果为0的时候停止，但除尾数是5的情况，其他情况都不会为0，也就是说*2永远不可能消灭小数部分，这样算法将无限下去。很显然，小数的二进制表示有时是不可能精确的。这也就解释了为什么浮点型减法出现了”减不尽”的精度丢失问题。

4. 合并结果：整数部分+小数部分，最终得到二进制结果为0.111。

所以该结果按照尾数 + 阶码的计算机计数方式，可以表示为：1.11 * 2 ** -1

对应位：

• 符号位（S）：0。
• 阶码（E）：若以float为例，应为127 + （-1） = 126，因此，二进制表示为：01111110
• 尾数部分（M）：若以float为例，应为23位，因此尾部补齐后为11000000000000000000000

因此，最终的结果为（以32位精度float表示）：00111111011000000000000000000000。

把十进制小数6.36转换成二进制

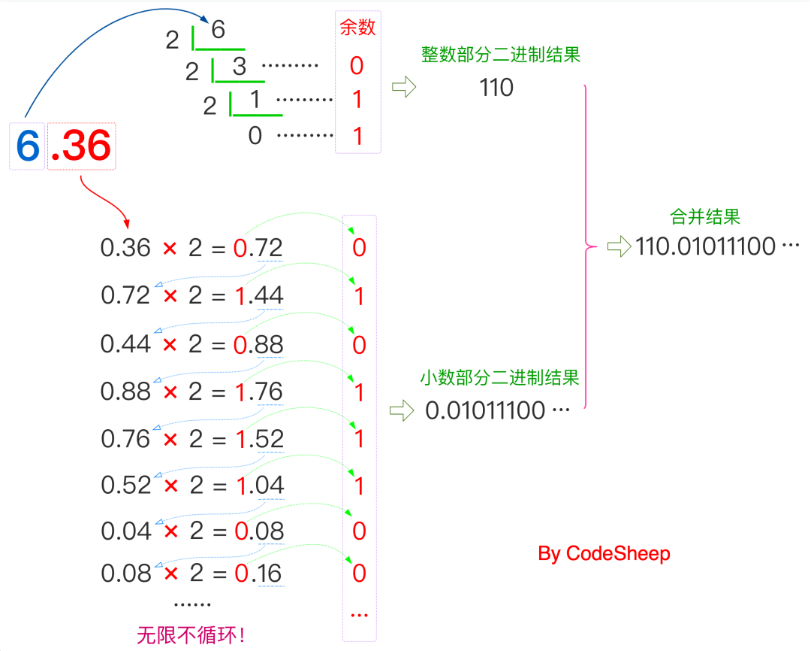
整数部分 + 小数部分，因此最终得到的结果二进制结果为 110.01011100…。

按照尾数 + 阶码的计算机计数方式，则可以表示为：1.1001011100… *2**2

对应位：

• 符号位（S）： 0
• 阶码（E）：若以float为例，应为127 + （2） = 129，因此，二进制表示为：10000001
• 尾数部分（M）：1001011100…，其实它本身无限不循环，但若以float型精度来截取23位，则可以表示为10010111000010100011111

因此最终的总结果为（以32位精度float表示）：01000000110010111000010100011111。

所以像这种无限位数的尾数情况，用计算机存储产生截取是必然的，必定会有一定的精度损失！所以这也从根本上解释了为什么float或者double这种类型数据使用时的风险性，因此必须要结合实际业务理性考量。