布隆过滤器简介
背景
在开发以及数据处理过程中,我们经常要判断一个元素是否在一个集合中,或者对一批元素去重,最直接的办法是是将所有元素存在计算机中,遇到新的元素时,将它和集合中的元素比较即可,当集合小时这样做快速准确,但当集合规模巨大时,因为要耗费存储空间,其存储效率低的问题的就显现出来。
比如:5TB的硬盘上放满了数据,请写一个算法将这些数据进行排重。如果这些数据是一些32bit大小的数据该如何解决?如果是64bit的呢?
如果数据全部放入内存,则需要 4字节 * 2的32次方 = 16GB 内存,显然这是不能接受的,有没有其他办法呢
有,使用 bitmap,只需要 1bit * 2的32次方 = 512MB,显然又可以了,但是如果是 64 位的呢,bitmap 需要 1bit * 2的64次方 = 2048PB = 2EB,明显也是不能接受的。
接下来要引入另一个著名的工业实现——布隆过滤器(Bloom Filter)
什么是布隆过滤器
布隆过滤器(Bloom Filter)是由伯顿·布隆(Burton Bloom)于1970年提出的。
它实际上是一个很长的二进制向量和一系列随机映射函数。可以用来告诉你 “某样东西一定不存在或者可能存在”。
工作原理
假定存储一亿个元素,先建立一个16亿个比特位即2亿字节的向量,然后将这16亿个比特位全部清零。
对于每一个元素X,用8个不同的随机数产生器 F1, F2, ..., F8 产生8个信息指纹 f1, f2, ..., f8,再将这8个信息指纹映射到1-16亿中的8个自然数 g1, g2, ..., g8。
现在将这8个位置的比特位全部设置为1。对这一亿个元素都进行这样的处理后,一个针对这些元素的布隆过滤器就建成了,如下图:
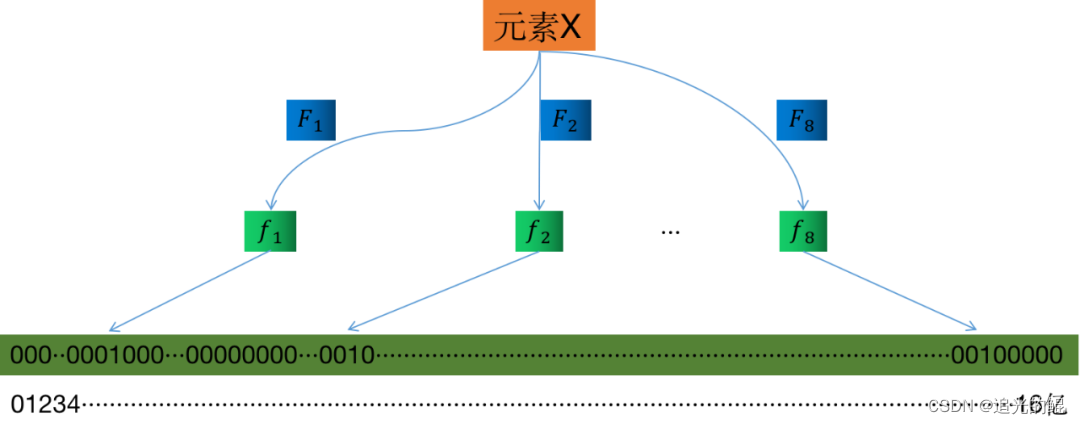
现在,来了一个新的元素Y,判断这个元素在不在过滤器中。
用相同的8个随机数生成器产生8个信息指纹,然后对应到布隆过滤器的8个比特位,如果Y在过滤器中,显然,其对应的8个比特值一定是1,如果对应的8个比特值不全是1,那么Y一定不在过滤器中。
布隆过滤器判断一个元素不存在,那么一定不存在。但是,他有个不足之处,即有极小的可能将一个不存在的元素判定为存在,因为可能某个不存在的元素在布隆过滤器中对应的8个位置“恰巧”被其他元素设置成1,我们把这种可能性称为误识别率。
这里有三个相关的推导公式用,假设需要过滤的元素个数为n,布隆过滤器的大小为m,所容忍的误识别率为p,随机数生成器(哈希函数)的个数为k。公式如下(小数向上取整):
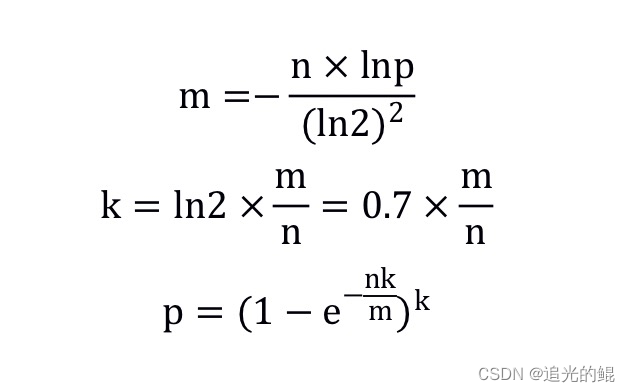
由于我们计算的m和k可能是小数,那么需要经过向上取整,此时需要重新计算误判率p!
所以在使用的时候需要注意:
- 使用时不要让实际元素数量远大于初始化数量;
- 当实际元素数量超过初始化数量时,应该对布隆过滤器进行重建,重新分配一个 size 更大的过滤器,再将所有的历史元素批量导入。
布隆过滤器的使用场景
利用布隆过滤器减少磁盘 IO 或者网络请求,因为一旦一个值必定不存在的话,就可以直接结束查询,比如以下场景:
- 大数据去重;
- 网页爬虫对 URL 的去重,避免爬取相同的 URL 地址;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
- 缓存击穿,将已存在的缓存放到布隆中,当黑客访问不存在的缓存时迅速返回避免缓存及数据库挂掉。