03-排序

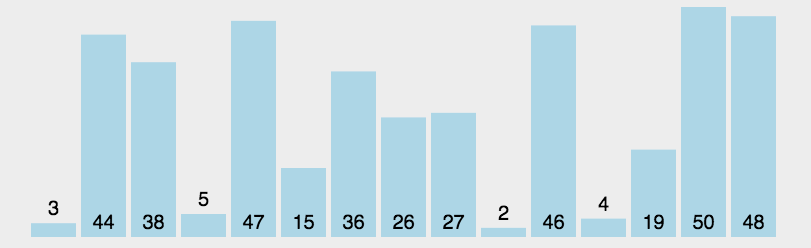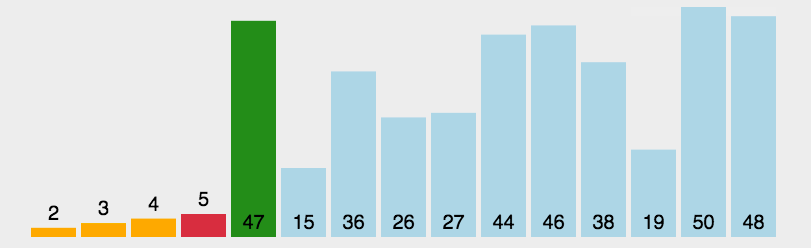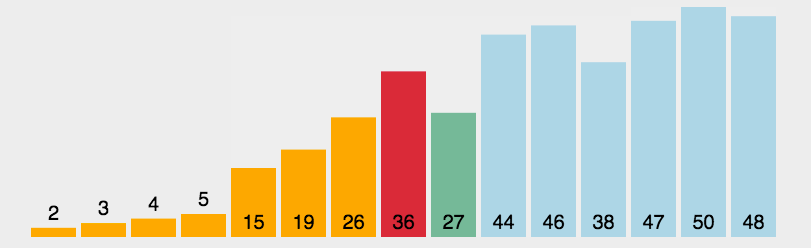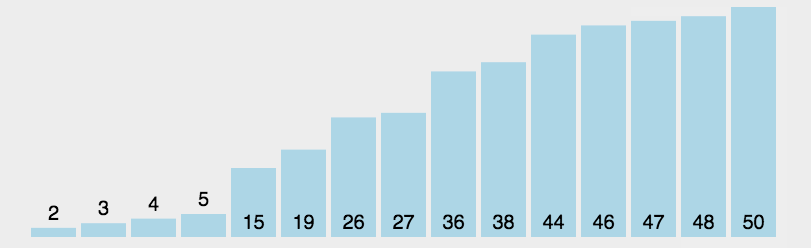
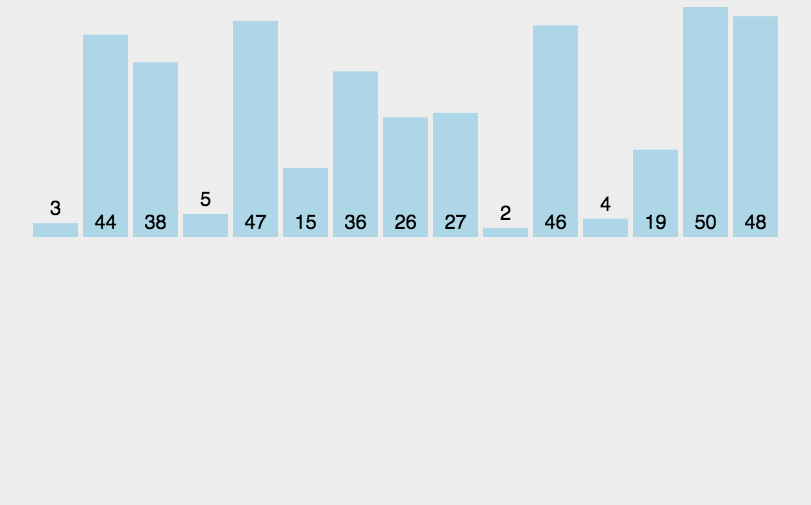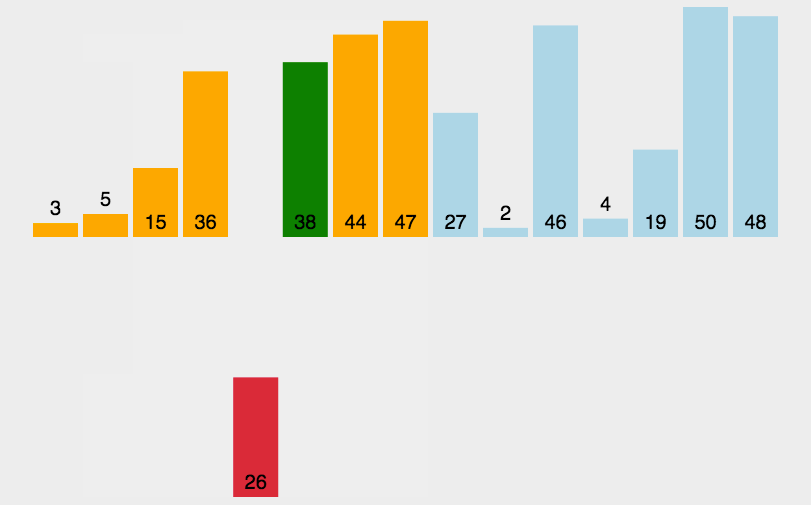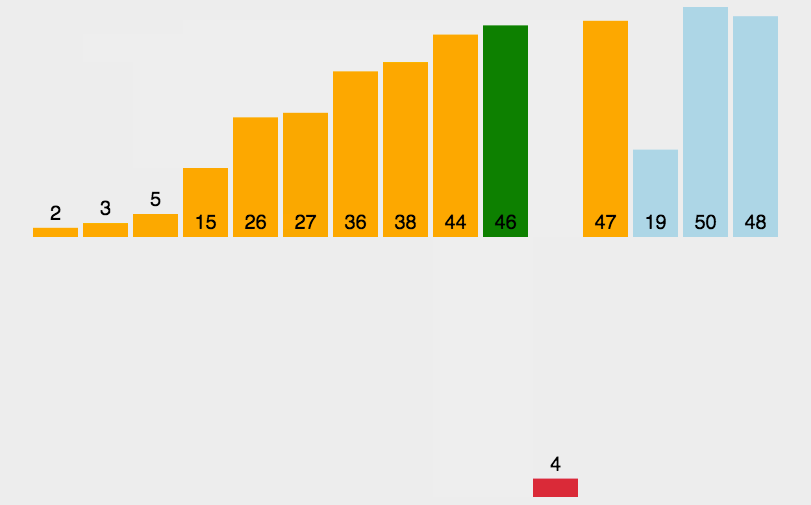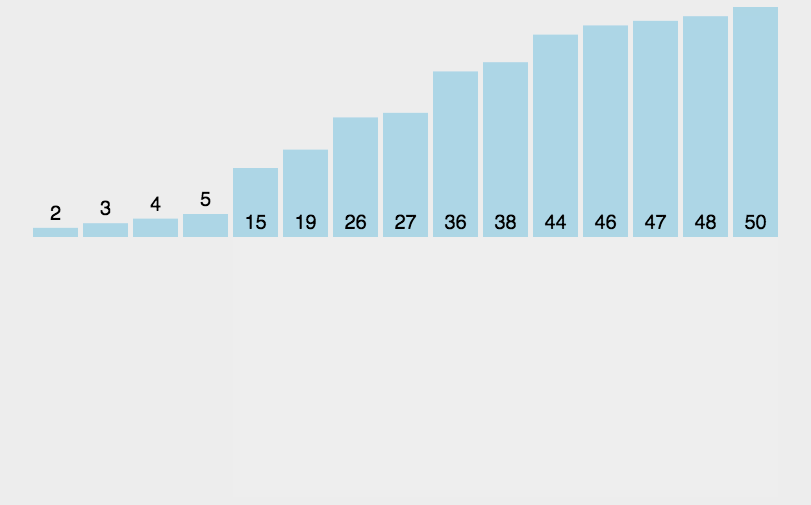
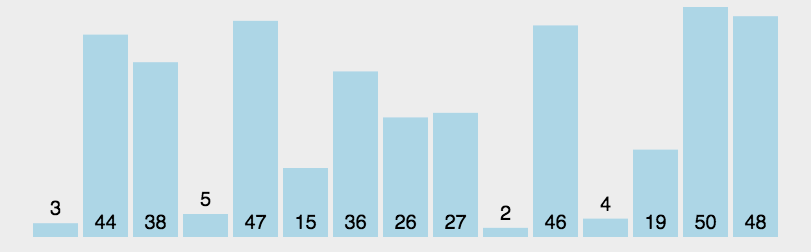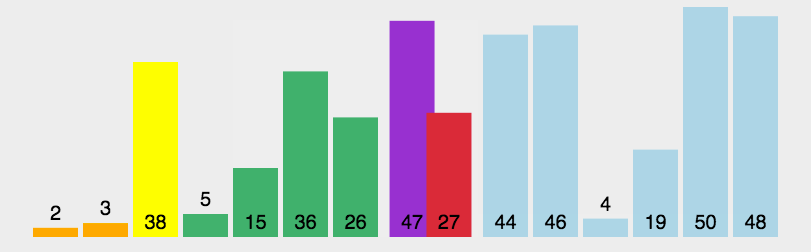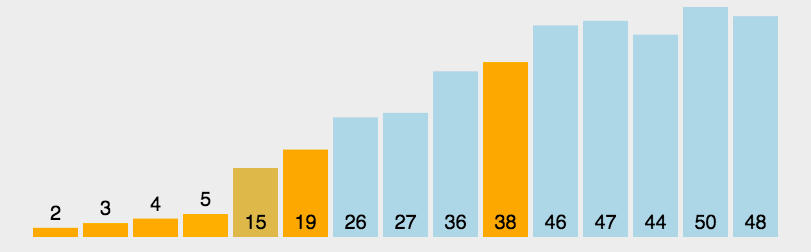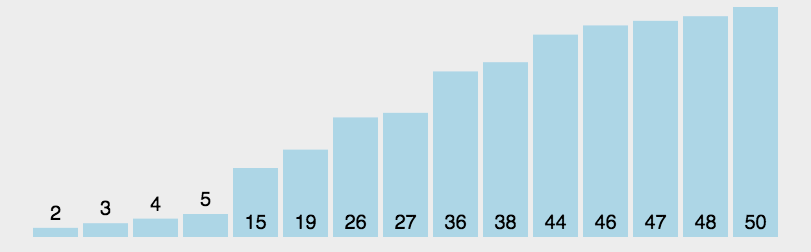
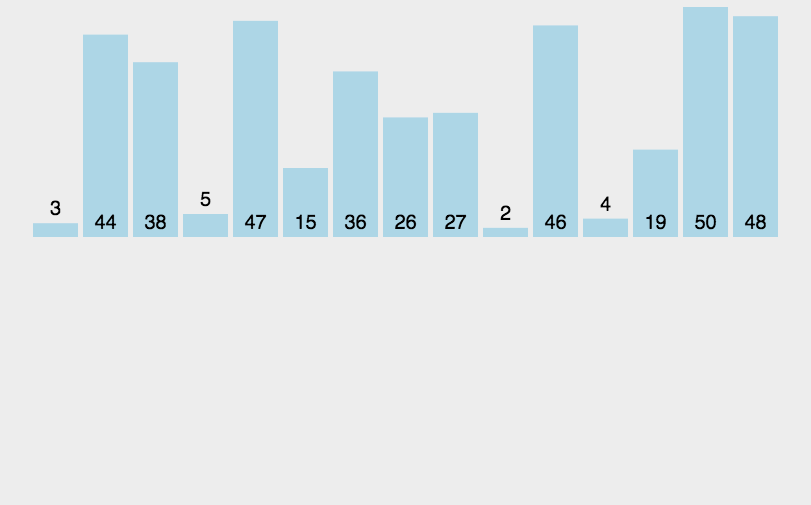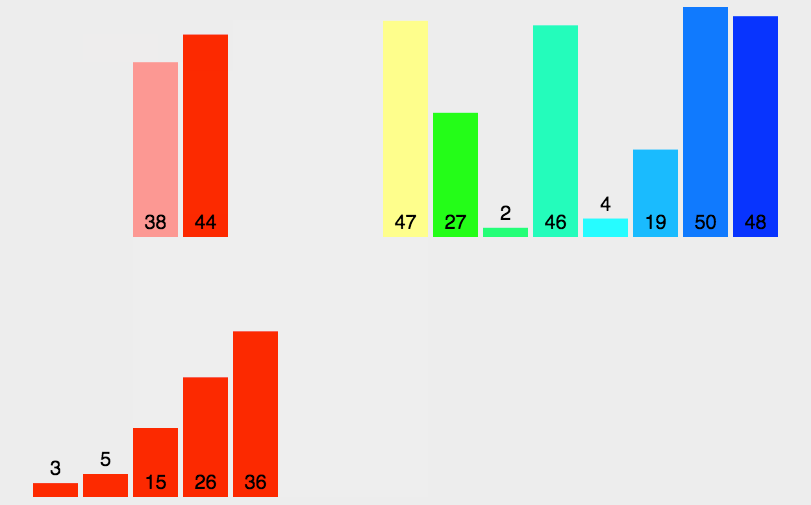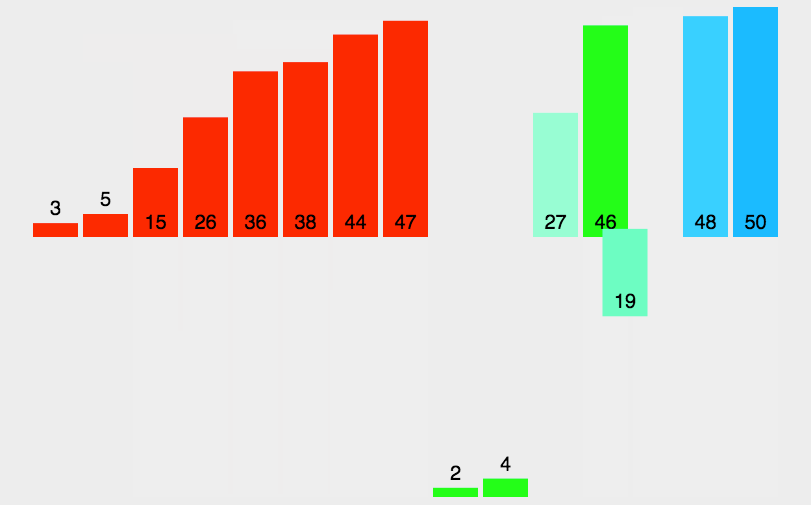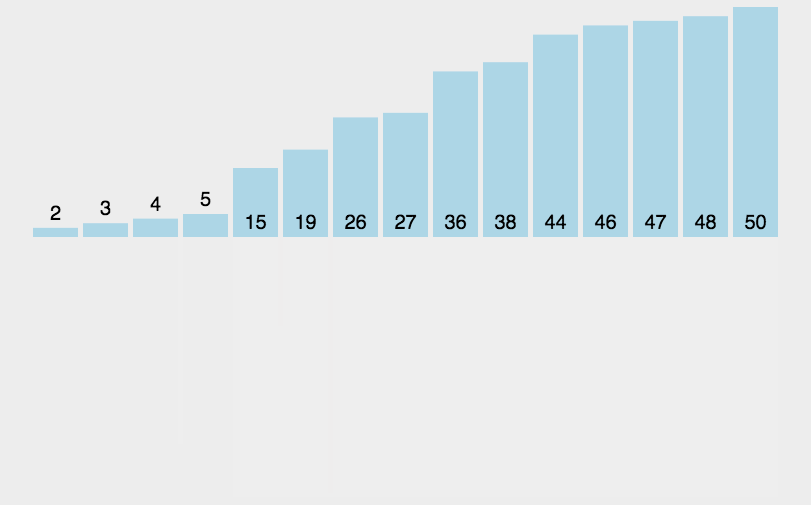
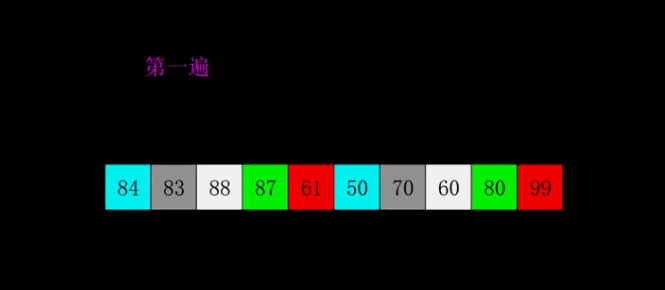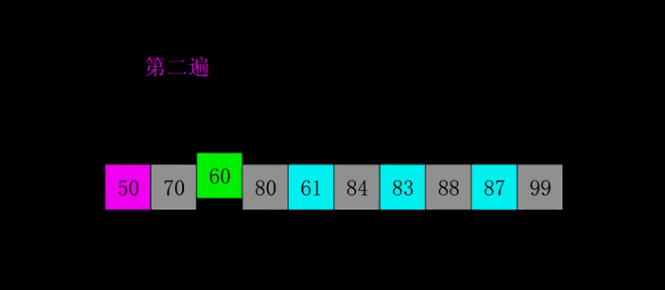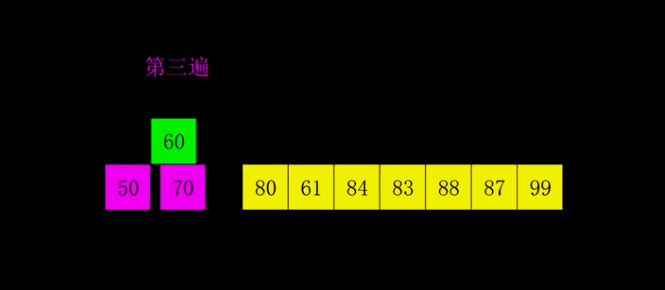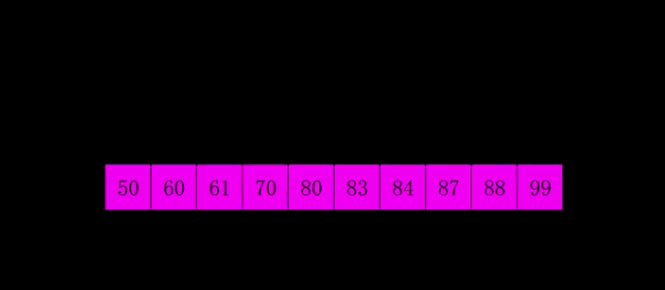
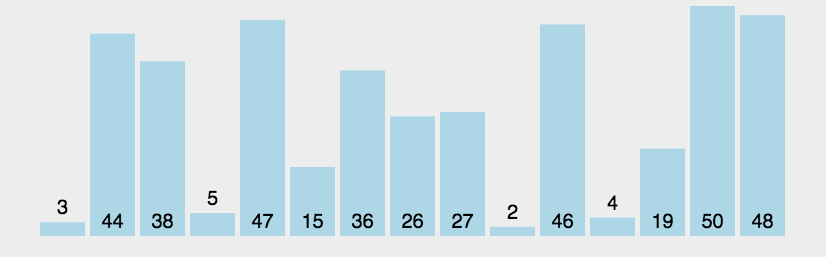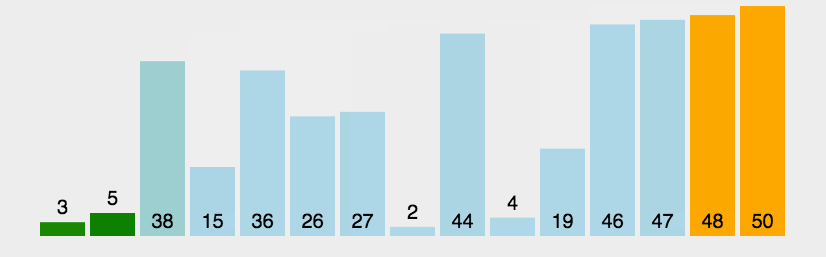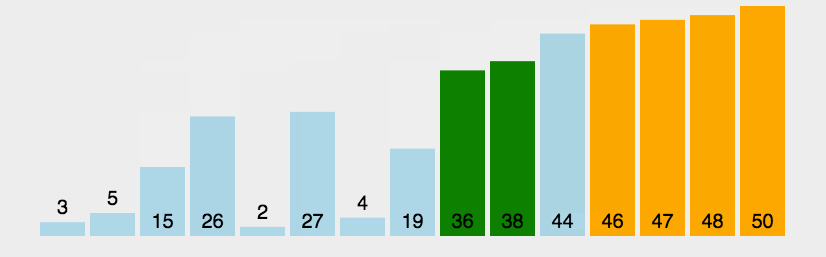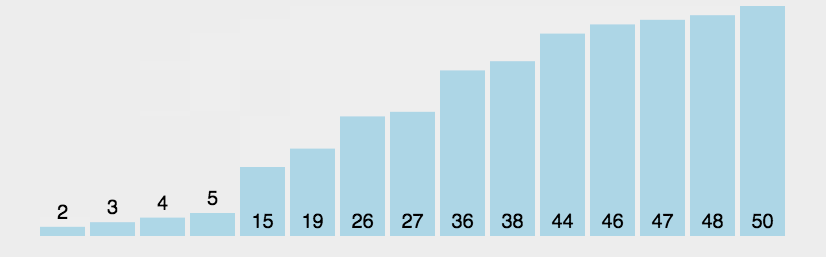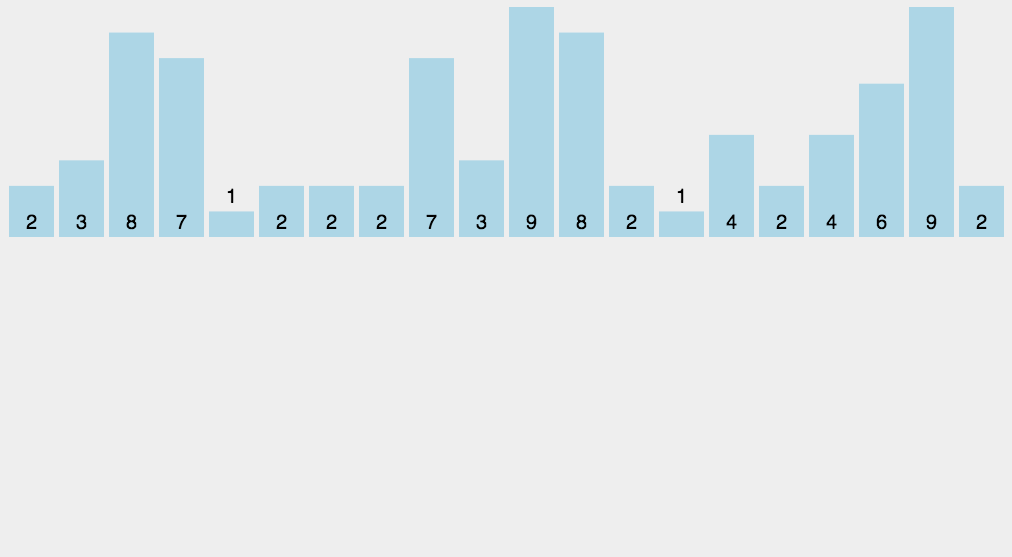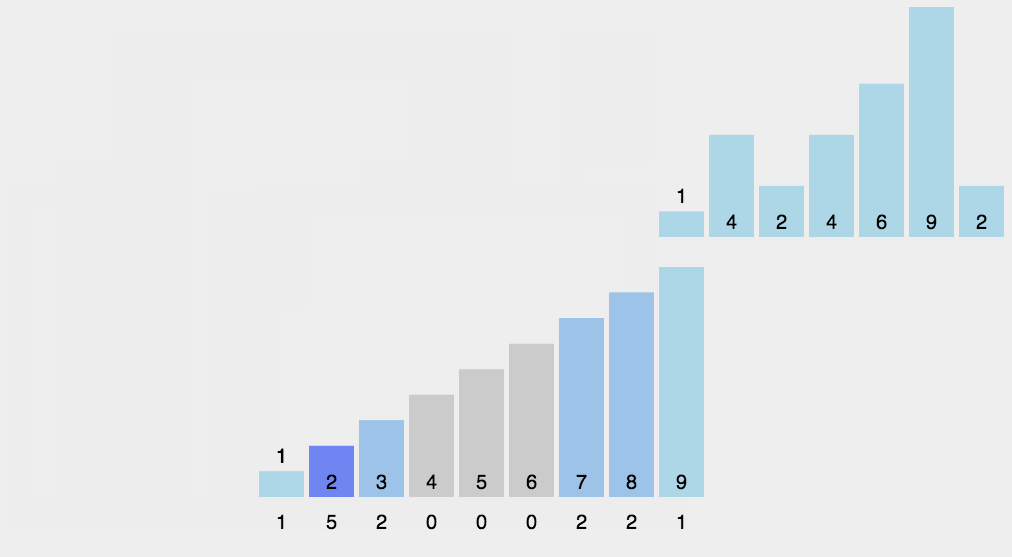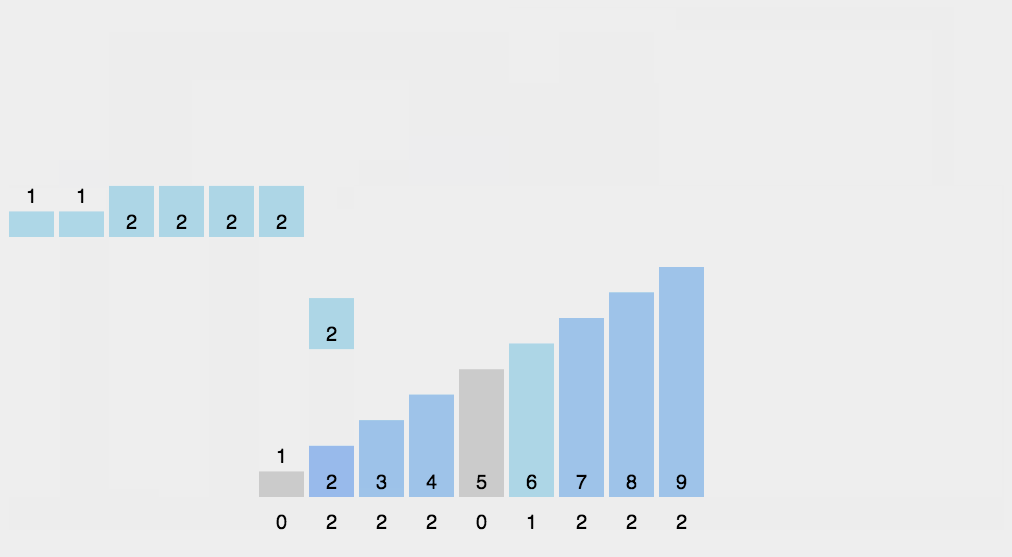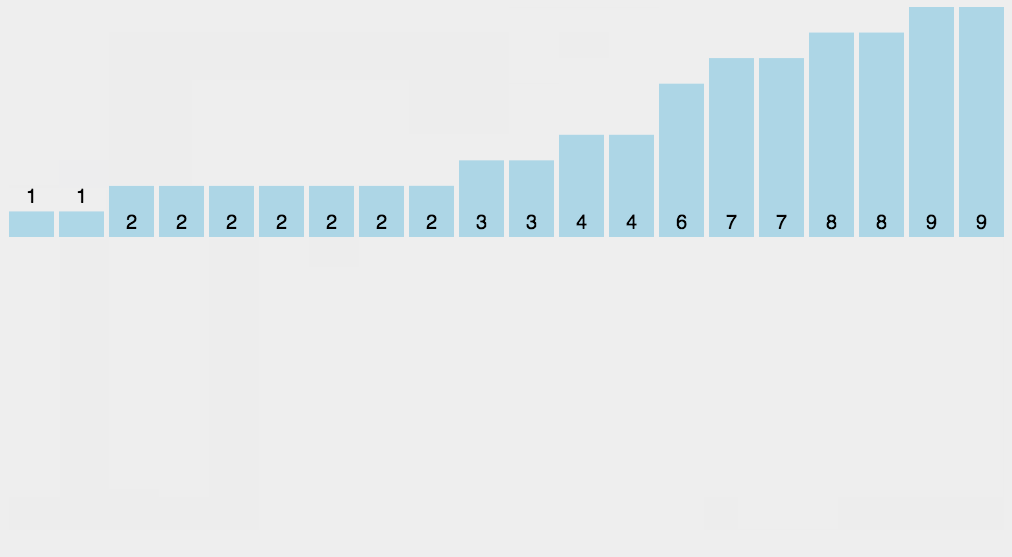冒泡排序（Bubble Sort）

• 时间复杂度：最优时间复杂度：O(n)，最坏时间复杂度：O(n²)。
• 优点：稳定，简单
• 缺点：效率不很高，运行时间较长

原理如下：

1. 比较相邻的元素，如果第一个比第二个大，就交换他们两个；
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。做完以后，最后的元素会是最大的数，这里可以理解为走了一趟；
3. 针对所有的元素重复以上的步骤，除了最后一个；
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较，最后数列就是从大到小一次排列；

代码实现

def bubble_sort(data):
    """
    冒泡排序
    :param data: 
    :return: 
    """
    for i in range(len(data)-1):  # 趟数
        for j in range(len(data)-i-1):  # 遍历数据，依次交换
            if data[j]>data[j+1]:  # 当较大数在前面
                data[j],data[j+1]=data[j+1],data[j] #交换两个数的位置

优化版本：当某一趟走完以后发现并没有进行数据交换，那么此时的数列已经排列好了，没有必要在进行下去。例如：极端情况下，数列本来已经排序好的，我们只需要走一趟即可完成排序。

def bubble_sort(data):
    """
    冒泡排序优化版
    :param data: 
    :return: 
    """
    for i in range(len(data)-1):  # 趟数
        exchange=False   # 交换标志
        for j in range(len(data)-i-1):  # 遍历数据，依次交换
            if data[j]>data[j+1]:  # 当较大数在前面
                data[j],data[j+1]=data[j+1],data[j]  # 交换两个数的位置
                exchange = True  # 改变标志
        if not exchange: # 如果某一趟没有进行交换，代表排序完成
            break
    return i  # 返回次数的趟数

选择排序（Selection Sort）

• 时间复杂度：最优时间复杂度：O(n²)；最坏时间复杂度：O(n²)
• 稳定性：不稳定
• 优点：移动次数少
• 缺点：比较次数多

工作原理

1. 每一次从待排序的列表中选出一个元素，并将其与其他数依次比较，若列表中的某个数比选中的数小，则交换位置，把所有数比较完毕，则会选出最小的数，将其放在最左边（这一过程称为一趟）；
2. 重复以上步骤，直到全部待排序的数据元素排完；

实现

def select_sort(data):
    """
    选择排序
    :param data: 待排序的数据列表
    :return: 
    """
    for i in range(len(data)-1):  #趟数
        min_index=i  # 记录i趟开始最小的数的索引，我们从最左边开始
        for j in range(i+1,len(data)): # 每一次趟需要循环的次数
            if data[j] < data[min_index]:  # 当数列中的某一个数比开始的数要小时候，更新最小值索引位置
                min_index=j
        data[i],data[min_index]=data[min_index],data[i]  # 一趟走完，交换最小值的位置，第一趟最小

插入排序（Insert Sort）

• 时间复杂度：最优时间复杂度：O(n)；最坏时间复杂度：O(n²)
• 稳定性：稳定
• 优点：稳定，比较快
• 缺点：比较次数不确定，数据量越大，该算法越渣

工作原理如下：

1. 以从小到大排序为例，元素 0 为第一个元素，插入排序是从元素 1 开始，尽可能插到前面。
2. 插入时分插入位置和试探位置，元素 i 的初始插入位置为 i，试探位置为 i-1，在插入元素i时，依次与 i-1,i-2… 元素比较，如果被试探位置的元素比插入元素大，那么被试探元素后移一位，元素 i 插入位置前移 1 位，直到被试探元素小于插入元素或者插入元素位于第一位。
3. 重复上述步骤，最后完成排序

实现

def insert_sort(data):
    """
    插入排序
    :param data: 待排序的数据列表
    :return: 
    """
    for i in range(1, len(data)): # 无序区域数据
        tmp = data[i] # 第i次插入的基准数
        for j in range(i, -1, -1):
            if tmp < data[j - 1]:  # j为当前位置，试探j-1位置
                data[j] = data[j - 1]  #  移动当前位置
            else:  # 位置确定为j
                break
        data[j] = tmp  # 将当前位置数还原

快速排序（Quick Sort）

• 时间复杂度：
• 最优时间复杂度：O(nlogn)遍历每个数是O(n)，访问每个数是O(logn)，最终是O(nlogn)可以转换为求二叉树深度的思想
• 最坏时间复杂度：O(n²)
• 稳定性：不稳定
• 优点：效率高，数据移动比较少，数据量越大，优势越明显
• 缺点：不稳定

快速排序（Quicksort），又称划分交换排序（partition-exchange sort）。通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序。

整个排序过程可以递归进行，以此达到整个数据变成有序序列。

工作原理如下：

1. 从数列中随机挑选出一个数作为基数；
2. 重新排列数列，使得比基数小的元素在左边，比基数大元素在右边，相等的元素放左边或者右边都可以，最后使得该基数在处于数列中间位置，这个称为分区操作；
3. 递归上述操作，完成排序

实现

def quick_sort(data,left,right):
    """
    快速排序
    :param data: 待排序的数据列表
    :param left: 基准数左边元素的索引
    :param right: 基准数右边元素的索引
    :return: 
    """
    if left < right:
        mid = partition(data,left,right)  # 分区操作,mid代表基数所在的索引
        quick_sort(data,left,mid-1)   # 对基准数前面进行排序
        quick_sort(data,mid+1,right)  # 对基准数后面进行排序
 
 
def partition(data,left,right):
    tmp=data[left]  # 随机选择的基准数,从最左边开始选
    while left < right:
        while left < right and data[right] >= tmp:  # 右边的数比基准数大
            right-=1  # 保留该数，然后索引指针往左移动
        data[left]=data[right]   # 否则此时右边数比基数小，则将该数放到基准位置
        while left < right and data[left] <= tmp: # 右边的数比基准数小
            left+=1  # 此时保持该数位置不动，索引指针往前移动
        data[right]=data[left]  # 否则此时左边的数比基数大，则将该数放到右边
    data[left] = tmp  # 最后将基准数量放回中间
    return left  # 返回基准数位置

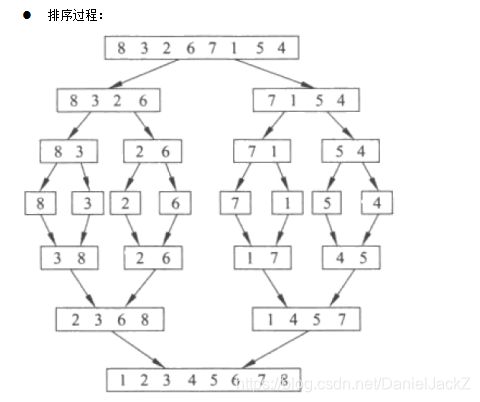
归并排序（Merge Sort）

• 最优时间复杂度：O(nlogn) 最坏时间复杂度：O(nlogn)
• 稳定性：稳定
• 优点：稳定，数据量越大越优秀
• 缺点：需要额外空间

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

归并排序是一种稳定的排序方法。和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(nlogn）的时间复杂度。代价是需要额外的内存空间。

工作原理如下：

• 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
• 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
• 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
• 重复步骤3直到某一指针达到序列尾；
• 将另一序列剩下的所有元素直接复制到合并序列尾

实现

def merge(data, low, mid, high):
    """
    合并函数
    :param data: 数据列表
    :param low: 列表开头位置
    :param mid: 分割中间位置
    :param high: 列表最后位置
    :return: 
    """
    i = low  # 第一个指针
    j = mid + 1  # 第二个指针
    tmp = []  # 临时存放的列表
    while i <= mid and j <= high:  # 分割的列表当两边都有数才进行
        if data[i] < data[j]:
            tmp.append(data[i])
            i += 1  # 低的指针往右移动
        else:
            tmp.append(data[j])  # 右边大，存右边的数
            j += 1  # 同时指针右移动
 
    while i <= mid:  # 左边分割有剩下
        tmp.append(data[i])
        i += 1
    while j <= high:  # 右边有剩下
        tmp.append(data[j])
        j += 1
    data[low:high + 1] = tmp  # 最后将tmp中的数写入到原来的列表中
 
 
def merge_sort(data, low, high):
    """
    归并排序
    :param data: 待排序的数据列表
    :param low: 数据列表开始位置
    :param high: 数据列表结束位置
    :return: 
    """
    if low < high:  # 至少有两个元素才进行
        mid = (low + high) // 2  # 分割
        merge_sort(data, low, mid)  # 递归分割上一部分
        merge_sort(data, mid + 1, high)  # 递归分割下一部分
        merge(data, low, mid, high)  # 合并

堆排序（Heap Sort）

• 时间复杂度：最优时间复杂度：O(nlogn)，最坏时间复杂度：O(nlogn)
• 稳定性：不稳定

本质是一个完全二叉树，如果根节点的值是所有节点的最小值称为小根堆，如果根节点的值是所有节点的最大值，称为大根堆。

原理：

1. 将待排序数据列表建立成堆结构(建立堆)；
2. 通过上浮(shift_up)或下沉(shift_down)等操作得到堆顶元素为最大元素（已大根堆为例）；
3. 去掉堆顶元素，将最后的一个元素放到堆顶，重新调整堆，再次使得堆顶元素为最大元素（相比第一次为第二大元素）；

• 重复3操作，直到堆为空，最后完成排序；

# -*- coding:utf8 -*-
import random
 
 
def sift(li, low, high):
    # li表示树, low表示树根, high表示树最后一个节点的位置
    tmp = li[low]
    i = low
    j = 2 * i + 1 # 初识j指向空位的左孩子
    # i指向空位,j指向两个孩子
    while j <= high: # 循环退出的第二种情况: j>high,说明空位i是叶子节点
        if j + 1 <= high and li[j] < li[j+1]: #如果右孩子存在并且比左孩子大,指向右孩子
            j += 1
        if li[j] > tmp:
            li[i] = li[j]
            i = j
            j = 2 * i + 1
        else: # 循环退出的第一种情况:j位置的值比tmp小,说明两个孩子都比tmp小
            break
    li[i] = tmp
 
 
def heap_sort(li):
    n = len(li)
    # 1. 构造堆
    for low in range(n//2-1, -1, -1):
        sift(li, low, n-1)
    # 2. 挨个出数
    for high in range(n-1, -1, -1):
        li[0], li[high] = li[high], li[0]
        sift(li, 0, high-1)
 
import copy
 
li = list(range(1000))
random.shuffle(li)
heap_sort(li)
print(li)

希尔排序（Shell Sort）

• 最优时间复杂度：根据步长序列的不同而不同，最优是1.3，根据数学运算算出的gap
• 最坏时间复杂度：O(n²)
• 稳定性：不稳定
• 优点：平均时间短，数据移动少
• 缺点：不稳定

希尔排序是插入排序的一种，也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法，是DL．Shell于1959年提出的。

工作原理如下：

1. 先取一个小于 n 的整数 d1 作为第一个增量，把文件的全部记录分组。所有距离为 d1 的倍数的记录放在同一个组中。
2. 先在各组内进行直接插入排序；
3. 取第二个增量 d2<d1 重复上述的分组和排序，直至所取的增量 =1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

def shell_sort(data):
    """
    希尔排序
    :param data:待排序的数据列表 
    :return: 
    """
    d1 = len(data) // 2  # 设置分割大小为d1，
    while d1 > 0:
        for i in range(d1, len(data)):  # 在插入排序中 d1 为 1
            tmp = data[i]  # 当前分割元素位置
            j = i - d1  # 上一个分割元素位置
            while j >= 0 and tmp < data[j]:  # 上一个元素分割位置比当前分割位置要大，则需要调整位置
                data[j + d1] = data[j]  # 后移动当前分割元素位置
                j -= d1  # 往前移d1
            data[j + d1] = tmp
        d1 //= 2  # 继续分割

计数排序（Count Sort）

• 时间复杂度：最优时间复杂度：O(n)，最坏时间复杂度：O(n)
• 稳定性：稳定
• 优点：速度快
• 缺点：有局限性，范围不能太大，只能是整数

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)，其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。

算法描述

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

def count_sort(li, max_num):
    count = [0 for i in range(max_num + 1)]  #设置计数序列并初始化为0
    for num in li:
        count[num] += 1
    i = 0
    for num,m in enumerate(count):
        for j in range(m):
            li[i] = num
            i += 1

桶排序（Bucket Sort）

• 时间复杂度：最优时间复杂度：O(n)，最坏时间复杂度：O(n)
• 稳定性：稳定
• 缺点：如果数据分布集中，如只分布在一个桶，效果不好。需要额外空间

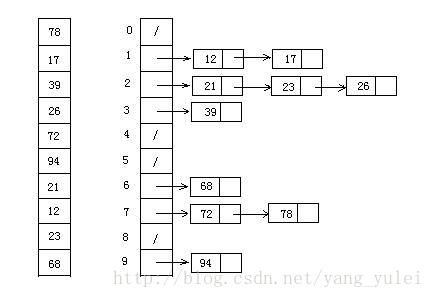
桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

算法描述

• 设置一个定量的数组当作空桶；
• 遍历输入数据，并且把数据一个一个放到对应的桶里去；
• 对每个不是空的桶进行排序；
• 从不是空的桶里把排好序的数据拼接起来。

def bucket_sort(data):
    buckets = [0] * ((max(data) - min(data)) + 1)  # 初始化桶元素为0
    for i in range(len(data)):
        buckets[data[i] - min(data)] += 1  # 遍历数组a，在桶的相应位置累加值
 
    ret_data = []
    for i in range(len(buckets)):
        if buckets[i] != 0:
            ret_data += [i + min(data)] * buckets[i]
    print(ret_data)
    return ret_data

基数排序（Radix Sort）

• 时间复杂度：最优时间复杂度：O(n)，最坏时间复杂度：O(n)
• 稳定性：稳定
• 缺点：只能处理正整数。需要额外空间

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的。

基数排序的空间复杂度为O(n+k)，其中k为桶的数量。一般来说n>>k，因此额外空间需要大概n个左右。

算法描述

• 取得数组中的最大数，并取得位数；
• arr为原始数组，从最低位开始取每个位组成radix数组；
• 对radix进行计数排序（利用计数排序适用于小范围数的特点）；

def radix_sort(li):
    max_num = max(li)
    i = 0
    while (10 ** i <= max_num):
        buckets = [[] for _ in range(10)]
        for val in li:
            digit = val // (10 ** i) % 10
            buckets[digit].append(val)
        li.clear()
        for bucket in buckets:
            for val in bucket:
                li.append(val)
        i += 1

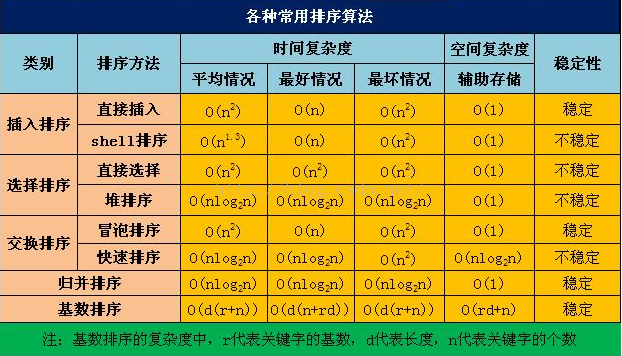
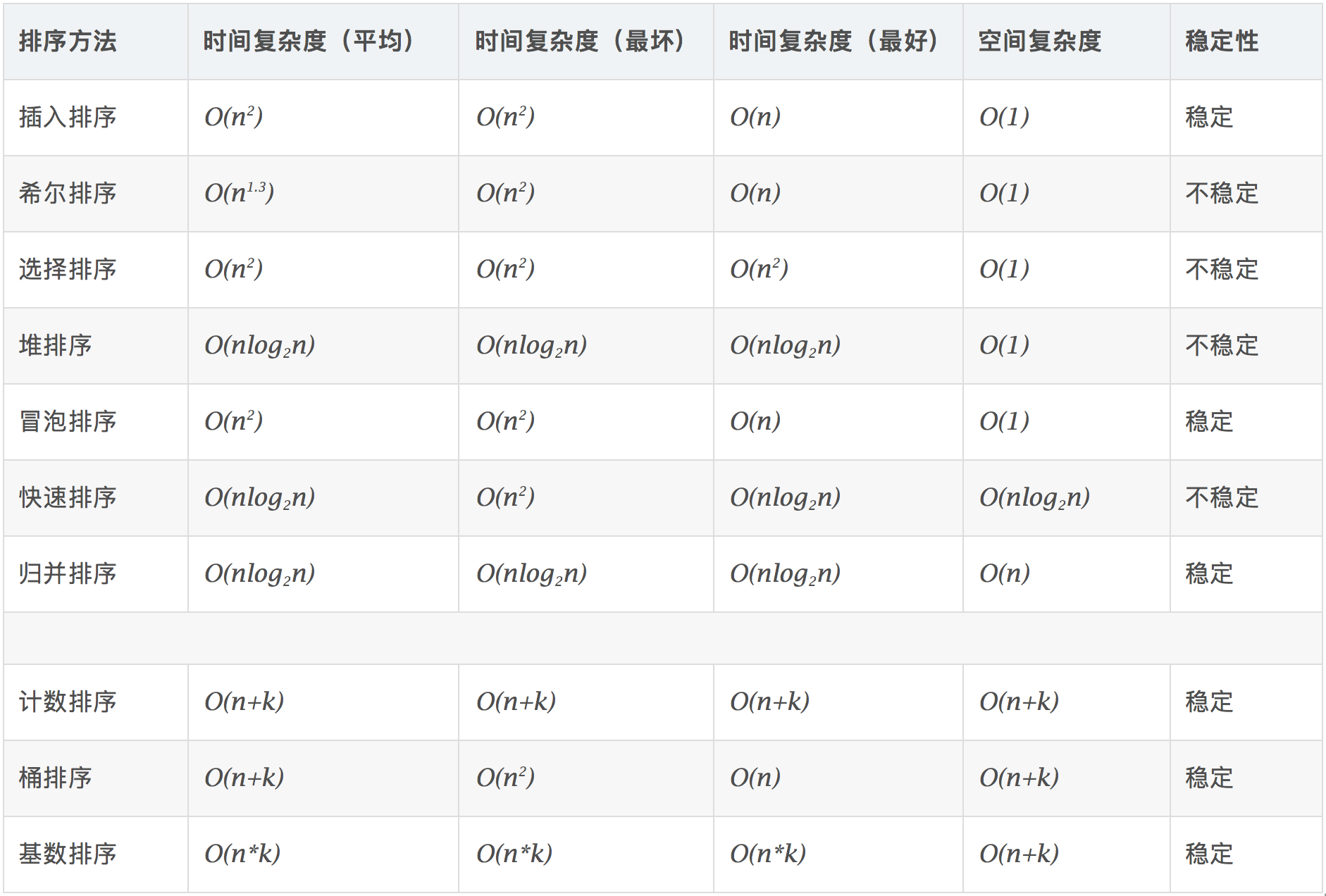
总结

十大经典排序算法（动图演示） - 一像素 - 博客园

Python算法基础 - W-D - 博客园

python实现常见算法_流浮生的博客-CSDN博客_python实现算法