bitmap

简介

位图（Bitmap），即位（Bit）的集合，是一种数据结构，可用于记录大量的 0-1 状态，在很多地方都会用到，比如 Linux 内核（如inode，磁盘块）、Bloom Filter算法等，其优势是可以在一个非常高的空间利用率下保存大量0-1状态。

BitMap 的原理

Bitmap 就是用一个bit位来标记某个元素对应的 Value， 而 Ke y即是该元素。由于采用了 Bit 为单位来存储数据，因此在存储空间方面，可以大大节省。

例如，存储 1, 3，5 这三个数值, 对应的位值为 1，表示该值存在。

0 1 0 1 0 1 0 0 0 
-----------------
0 1 2 3 4 5 6 7 8

BitMap 算法处理大数据问题的场景

1. 给定10亿个不重复的正 int 的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那10亿个数当中。

   • 解法：遍历10个亿数字，映射到 BitMap 中，然后对于给出的数，直接判断指定的位上存在不存在即可。

2. 使用位图法判断正整形数组是否存在重复

   • 解法：遍历一遍，存在之后设置成 1，每次放之前先判断是否存在，如果存在，就代表该元素重复。

3. 使用位图法进行元素不重复的正整形数组排序

   • 解法：遍历一遍，设置状态1，然后再次遍历，对状态等于1的进行输出，参考计数排序的原理。

4. 在2.5亿个整数中找出不重复的正整数，注，内存不足以容纳这2.5亿个整数

   • 解法1：采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）。

   • 解法2：采用两个BitMap，即第一个Bitmap存储的是整数是否出现，接着，在之后的遍历先判断第一个BitMap里面是否出现过，如果出现就设置第二个BitMap对应的位置也为1，最后遍历BitMap，仅仅在一个BitMap中出现过的元素，就是不重复的整数。

   • 解法3：分治+Hash取模，拆分成多个小文件，然后一个个文件读取，直到内存装的下，然后采用Hash+Count的方式判断即可。

   • 该类问题的变形问题，如已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。8位最多 99 999 999，大概需要 99m 个 bit，大概 10几m字节的内存即可。（可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要99M个Bit==12MBytes，这样，就用了小小的12M左右的内存表示了所有的8位数的电话）

5. 5TB的硬盘上放满了数据，请写一个算法将这些数据进行排重。如果这些数据是一些 32bit 大小的数据该如何解决？如果是 64bit 的呢？

   • 解法：32 bit 大小即 2 ** 32 bit = 4Gbit = 0.5 GB = 512MB， 完全可以放的下。
   • 如果数据是 64 位的话，bitmap 解决不了，需要用到布隆过滤器。

BitMap 的一些缺点

1. 数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题，那就可以考虑用 Bloom Filter 来解决，Bloom Filter 使用多个 Hash 函数来减少冲突的概率。

2. 数据稀疏。又比如要存入(10,8887983,93452134)这三个数据，我们需要建立一个 99999999 长度的 BitMap ，但是实际上只存了3个数据，这时候就有很大的空间浪费，碰到这种问题的话，可以通过引入 Roaring BitMap 来解决。

Python 实现

由于算法储存数据的粒度到了位，因此代码中使用了很多位运算，先回顾一下 Python 中的位运算操作。

# 或运算
bin(10), bin(8)  # ('0b1010', '0b1000')
bin(10 | 8)      # '0b1010'

# 与预算
bin(10), bin(8)  # ('0b1010', '0b1000')
bin(10 & 8)      # '0b1000'

# 位移运算
bin(10)         # '0b1010'
bin(10 << 3)    # '0b1010000'

Python 代码实现思路

Python 中，整数一般使用四个字节（32位）存储。代码中使用 n 个 4 字节的整数来储存数据，每个整数有 4*8=32位，对于 Python 来说，整数类型默认是有符号类型，第一位为符号位，所以一个整数的可用位数为 31 位。所以每个整数实际可存储 31 个数据。

假定我们要储存的客户的ID，元素个数 n 根据需要储存的最大ID计算得到。

然后循环的把ID存储bitmap中，储存每个ID时，先计算ID对应的元素下标和在元素中的存在第几位。

例如我们要储存的 ID 是30，通过后面的 get_element_index 和 get_bit_index 函数的计算分别得到元素下标是0，储存位数是30。

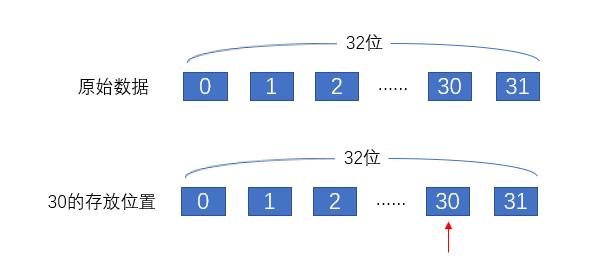
然后把第0个元素的第30位（从0开始）置为1即可。

代码

class BitMap(object):
    def __init__(self, max_value):
        """
        使用多个整型元素来储存数据，每个元素4个字节（32位）
        """
        self._size = int((max_value + 31 - 1) / 31)  # 计算需要的字节数，字节数也是数组的大小
        self.array = [0 for i in range(self._size)]  # 数组的元素都初始化为0，每个元素有32位

    @staticmethod
    def get_element_index(num):
        """
        获取该数即将储存的字节在数组中下标
        """
        return num // 31

    @staticmethod
    def get_bit_index(num):
        """
        获取该数在元素中的位下标
        """
        return num % 31

    def set(self, num):
        """
        将该数存在对应的元素的对应位置
        """
        element_index = self.get_element_index(num)
        bit_index = self.get_bit_index(num)
        self.array[element_index] = self.array[element_index] | (1 << bit_index)

    def find(self, num):
        """
        查找该数是否存在与bitmap中
        """
        element_index = self.get_element_index(num)
        bit_index = self.get_bit_index(num)
        if self.array[element_index] & (1 << bit_index):
            return True
        return False

    def count_one(self):
        """
        统计bitmap中数据的个数
        """
        count = 0
        for n in self.array:
            while n > 0:
                n = n & (n - 1)
                count += 1
        return count


def main():
    array_list = [30, 32, 5, 45, 2, 78, 35, 67, 90, 879, 0, 340, 123, 46, 1, 5]
    # 根据最大数的值创建BitMap对象
    bitmap = BitMap(max_value=max(array_list))

    # 将数据逐个存入bitmap
    for num in array_list:
        bitmap.set(num)

    # 查询数据是否存在于bitmap中
    results = []
    for i in range(max(array_list) + 1):
        if bitmap.find(i):
            results.append(i)
    print(results)


if __name__ == '__main__':
    main()

Reference

• https://www.freesion.com/article/11271095692/
• https://www.cnblogs.com/RioTian/p/14983524.html
• https://blog.csdn.net/keepaware/article/details/122202477